System binarny to podstawowy sposób reprezentowania liczb w informatyce, który wykorzystuje jedynie dwie cyfry: 0 i 1. Każda pozycja w liczbie binarnej odpowiada potędze liczby 2, co sprawia, że zrozumienie tego systemu jest kluczowe dla wielu dziedzin technologii. W tym artykule omówimy, jak przekształcać liczby dziesiętne na binarne oraz jak obliczać ich wartości w systemie dziesiętnym. Przedstawimy również zasady wykonywania podstawowych operacji arytmetycznych w systemie binarnym, takich jak dodawanie, odejmowanie, mnożenie i dzielenie.
Bez względu na to, czy jesteś studentem, programistą, czy po prostu ciekawym tematu, zrozumienie systemu binarnego otworzy przed Tobą nowe możliwości w świecie cyfrowym. Przygotuj się na przystępne wyjaśnienia i praktyczne przykłady, które pomogą Ci w opanowaniu tej istotnej umiejętności.
Kluczowe informacje:
- System binarny wykorzystuje tylko cyfry 0 i 1 do reprezentacji liczb.
- Aby zamienić liczbę dziesiętną na binarną, należy dzielić ją przez 2 i zapisywać reszty.
- Wartość liczby binarnej w systemie dziesiętnym oblicza się, sumując potęgi liczby 2 dla pozycji z cyfrą 1.
- Podstawowe zasady dodawania i odejmowania w systemie binarnym są podobne do tych w systemie dziesiętnym, z uwzględnieniem przeniesień i pożyczek.
- Mnożenie i dzielenie w systemie binarnym również mają swoje zasady, które można łatwo opanować.
Jak zamienić liczbę dziesiętną na binarną: Proste kroki konwersji
Konwersja liczby dziesiętnej na binarną jest prostym procesem, który można zrealizować poprzez dzielenie liczby przez 2. W tej metodzie, dzielimy liczbę, zapisując reszty z każdego dzielenia, co pozwala nam uzyskać wynik w systemie binarnym. Na przykład, aby przekształcić liczbę dziesiętną 13 na system binarny, dzielimy ją przez 2, co daje 6 z resztą 1. Kontynuujemy dzielenie 6 przez 2, co daje 3 z resztą 0, następnie 3 przez 2, co daje 1 z resztą 1, a na koniec 1 przez 2, co daje 0 z resztą 1. Ta metoda jest efektywna i łatwa do zastosowania.
Po zebraniu wszystkich reszt, ich kolejność ma znaczenie. Odczytujemy je w odwrotnej kolejności, co pozwala uzyskać ostateczny wynik w postaci liczby binarnej. W przypadku naszej liczby 13, reszty to 1, 0, 1, 1, co daje nam wynik 1101 w systemie binarnym. Ta technika jest fundamentalna dla zrozumienia, jak obliczyć system binarny i jest podstawą wielu operacji w informatyce.
Krok po kroku: Jak dzielić liczby przez 2 i zbierać reszty
Aby przeprowadzić konwersję liczby dziesiętnej na binarną, należy zacząć od podzielenia liczby przez 2. Każde dzielenie powinno być zapisywane razem z resztą. Na przykład, zaczynając od liczby 13, dzielimy ją przez 2, co daje nam 6, a reszta to 1. Następnie, dzielimy 6 przez 2, co daje 3 z resztą 0. Kontynuujemy ten proces, aż osiągniemy wynik 0. Kluczowe jest, aby na każdym etapie zapisywać reszty, ponieważ będą one użyteczne do uzyskania ostatecznego wyniku binarnego.
- Podziel liczbę przez 2 i zapisz resztę.
- Kontynuuj dzielenie, aż osiągniesz 0.
- Odczytaj reszty w odwrotnej kolejności, aby uzyskać wynik binarny.
Odczytywanie reszt: Jak odwrócić kolejność dla wyniku binarnego
Po zebraniu reszt z kolejnych dzielen, kluczowym krokiem jest ich odwrócenie, aby uzyskać finalny wynik w systemie binarnym. Gdy dzielimy liczbę dziesiętną przez 2, każda reszta reprezentuje jedną cyfrę w liczbie binarnej. Odczytując te reszty w odwrotnej kolejności, zaczynając od ostatniej zapisanej, tworzymy poprawną reprezentację binarną. Na przykład, jeśli reszty z dzielenia liczby 13 przez 2 to 1, 0, 1, 1, to po ich odwróceniu otrzymujemy 1101, co jest wynikiem w systemie binarnym.
Warto pamiętać, że kolejność reszt jest kluczowa dla uzyskania poprawnego wyniku. Zaczynamy od reszty uzyskanej z ostatniego dzielenia, a kończymy na pierwszej. To prosty, ale niezwykle ważny proces, który pozwala na skuteczne przekształcenie liczby dziesiętnej na binarną. Dzięki tej metodzie każdy może łatwo zrozumieć, jak obliczyć system binarny i wykorzystać tę wiedzę w praktyce.
Zasady potęg: Jak zrozumieć wartości pozycji w systemie binarnym
W systemie binarnym każda pozycja liczby odpowiada potędze liczby 2. Zaczynając od prawej strony, pierwsza pozycja to 2^0, następna to 2^1, potem 2^2, i tak dalej. Oznacza to, że wartość każdej cyfry w liczbie binarnej jest mnożona przez odpowiednią potęgę 2. Na przykład, w liczbie binarnej 1011, cyfra 1 na skrajnej lewej pozycji to 1 * 2^3, co daje 8, cyfra 0 na drugiej pozycji to 0 * 2^2, co daje 0, cyfra 1 na trzeciej pozycji to 1 * 2^1, czyli 2, a ostatnia cyfra 1 na skrajnie prawej pozycji to 1 * 2^0, co daje 1. Zrozumienie tych zasad jest kluczowe dla obliczania wartości liczby binarnej w systemie dziesiętnym.
Każda cyfra w systemie binarnym ma swoją wagę, która rośnie w miarę przesuwania się w lewo. Dlatego, gdy sumujemy wartości pozycji, uzyskujemy ostateczną wartość liczby w systemie dziesiętnym. Na przykład, dla liczby binarnej 1011, dodajemy wartości: 8 (z 2^3) + 0 (z 2^2) + 2 (z 2^1) + 1 (z 2^0), co daje 11 w systemie dziesiętnym. Zrozumienie tych zasad potęg jest niezbędne, aby efektywnie obliczyć system binarny i wykorzystać go w praktyce.
Przykłady konwersji: Jak obliczyć wartość liczby binarnej
Aby lepiej zrozumieć, jak obliczyć wartość liczby binarnej, przyjrzyjmy się kilku konkretnym przykładom. Na przykład, liczba binarna 1101 jest obliczana w następujący sposób: 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0, co daje 8 + 4 + 0 + 1, a w efekcie 13 w systemie dziesiętnym. Inny przykład to liczba 1010, która jest obliczana jako 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0, co daje 8 + 0 + 2 + 0, a w rezultacie 10 w systemie dziesiętnym.
| Liczba binarna | Wartość dziesiętna |
| 1010 | 10 |
| 1101 | 13 |
| 1110 | 14 |
| 1001 | 9 |
Jak wykonywać operacje arytmetyczne w systemie binarnym: Proste zasady
Operacje arytmetyczne w systemie binarnym są oparte na prostych zasadach, które różnią się od tych stosowanych w systemie dziesiętnym. Dodawanie binarne polega na łączeniu cyfr w taki sposób, że 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, a 1 + 1 = 10. W przypadku dodawania dwóch jedynek, wynik to 0 z przeniesieniem 1 do następnej pozycji. To przeniesienie jest kluczowe, ponieważ wpływa na wynik kolejnych działań. Na przykład, dodając 1101 (13 w systemie dziesiętnym) i 1011 (11 w systemie dziesiętnym), najpierw dodajemy skrajnie prawe cyfry, co daje 0, następnie 1 + 1, co daje 10, a następnie dodajemy kolejne cyfry z uwzględnieniem przeniesienia.
Oprócz dodawania, odejmowanie binarne również ma swoje zasady. Podobnie jak w systemie dziesiętnym, odejmowanie w systemie binarnym opiera się na pożyczkach. Na przykład, jeśli chcemy odjąć 1 od 0, musimy "pożyczyć" 1 z wyższej pozycji, co sprawia, że 0 staje się 10. W praktyce, jeśli odejmujemy 1010 (10 w systemie dziesiętnym) od 1100 (12 w systemie dziesiętnym), zaczynamy od prawej strony i, w przypadku braku wystarczającej wartości, wykonujemy pożyczki. Te zasady są fundamentalne dla zrozumienia, jak wykonywać operacje w systemie binarnym w codziennych obliczeniach.
Dodawanie binarne: Jak stosować zasady dodawania w praktyce
Aby dodać liczby binarne, należy stosować zasady dodawania, które są nieco inne niż w systemie dziesiętnym. Na przykład, rozważmy dodawanie dwóch liczb binarnych: 1010 (10 w systemie dziesiętnym) i 0110 (6 w systemie dziesiętnym). Zaczynamy od prawej strony: 0 + 0 = 0, następnie 1 + 1 = 10, co oznacza, że zapisujemy 0 i przenosimy 1 do następnej kolumny. W kolejnej kolumnie dodajemy 0 + 1 + 1 (przeniesienie), co daje 10, a więc znowu zapisujemy 0 i przenosimy 1. Na końcu dodajemy 1 (z przeniesienia) do 1, co daje 10, co zapisujemy jako 1 z nowym przeniesieniem. Ostateczny wynik to 10000, co odpowiada 16 w systemie dziesiętnym.
Odejmowanie binarne: Jak wykorzystać pożyczki w obliczeniach
Odejmowanie w systemie binarnym opiera się na zasadach, które są podobne do tych stosowanych w systemie dziesiętnym, z kluczowym elementem, jakim jest pożyczka. Kiedy próbujemy odjąć 1 od 0, musimy pożyczyć 1 z wyższej pozycji. Na przykład, jeśli mamy do odjęcia 1 od 0100 (4 w systemie dziesiętnym), musimy pożyczyć z drugiej pozycji, co zmienia 0100 w 0010 (2 w systemie dziesiętnym) i przekształca 0 w 10, co daje nam 1. W ten sposób możemy przeprowadzić odejmowanie, nawet gdy brakuje nam wartości w danej pozycji.
Przykładem może być odejmowanie 0110 (6 w systemie dziesiętnym) od 1001 (9 w systemie dziesiętnym). Zaczynamy od prawej strony: 1 - 0 = 1, następnie 0 - 1 wymaga pożyczki, więc przekształcamy 0 w 10, co daje 2 - 1 = 1. Kolejna kolumna to 0 - 1, co znowu wymaga pożyczki, więc przekształcamy 0 w 10, co daje 2 - 1 = 1. Ostatecznie w najstarszej kolumnie mamy 1 - 0 = 1. Wynik to 0011, co odpowiada 3 w systemie dziesiętnym. Zrozumienie tego procesu jest kluczowe dla efektywnego wykonywania operacji w systemie binarnym.
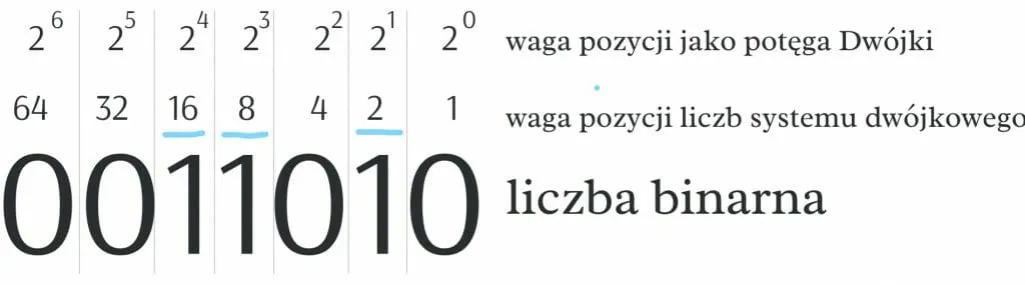
Czytaj więcej: Jak oszukać system binarny i uniknąć typowych błędów w obliczeniach
Jak mnożyć i dzielić liczby w systemie binarnym: Praktyczne przykłady
Mnożenie w systemie binarnym jest prostsze niż mogłoby się wydawać. Zasady są podobne do tych w systemie dziesiętnym, ale opierają się na podstawowych operacjach 0 i 1. Na przykład, aby pomnożyć 101 (5 w systemie dziesiętnym) przez 11 (3 w systemie dziesiętnym), wykonujemy mnożenie jak w systemie dziesiętnym, ale zamiast dziesiątek używamy potęg liczby 2. Zaczynamy od pierwszej cyfry 1, co daje 101, następnie dodajemy przesunięte 101 (odpowiadające drugiej cyfrze 1), co daje nam 1111, czyli 15 w systemie dziesiętnym.
Dzieląc liczby binarne, proces jest nieco bardziej skomplikowany, ale również oparty na znanych zasadach. Na przykład, dzieląc 1100 (12 w systemie dziesiętnym) przez 11 (3 w systemie dziesiętnym), zaczynamy od największej pozycji. 11 mieści się w 110, co daje 1, a następnie odejmujemy 11 od 110, co daje 1, a następnie przynosimy 0, co daje nam 100. Następnie 11 mieści się w 1000, co daje nam 10 w systemie dziesiętnym. Ostatecznie wynik dzielenia 1100 przez 11 to 10 w systemie binarnym.
Praktyczne zastosowania systemu binarnego w programowaniu i technologii
Znajomość systemu binarnego ma kluczowe znaczenie w wielu dziedzinach technologii, zwłaszcza w programowaniu i inżynierii komputerowej. Programiści często wykorzystują liczby binarne do tworzenia algorytmów, które są podstawą działania oprogramowania. Na przykład, rozumienie operacji binarnych jest niezbędne przy pracy z systemami zarządzania pamięcią, gdzie efektywne wykorzystanie bitów może znacząco poprawić wydajność aplikacji. W kontekście programowania niskopoziomowego, znajomość systemu binarnego pozwala na lepsze zrozumienie działania procesorów i architektur komputerowych, co jest niezbędne do optymalizacji kodu.
W przyszłości, z rozwojem technologii takich jak sztuczna inteligencja i uczenie maszynowe, umiejętność manipulowania danymi w systemie binarnym będzie jeszcze bardziej istotna. Na przykład, algorytmy oparte na sieciach neuronowych często operują na danych binarnych, co sprawia, że zrozumienie ich struktury oraz sposobu działania jest kluczowe dla efektywnego projektowania i implementacji tych systemów. W miarę jak technologia staje się coraz bardziej złożona, umiejętność pracy z systemem binarnym może otworzyć drzwi do nowych możliwości w obszarze innowacji i rozwoju technologicznego.

