Obliczanie systemu binarnego w Excelu może wydawać się skomplikowane, ale z odpowiednimi narzędziami staje się proste i intuicyjne. Kluczową funkcją, której użyjemy, jest DEC2BIN, która pozwala na konwersję liczb dziesiętnych na ich odpowiedniki w systemie binarnym. Wystarczy wpisać liczbę dziesiętną w jednej komórce, a następnie użyć formuły, aby uzyskać wynik w formacie binarnym.
W tym artykule dowiesz się, jak skutecznie korzystać z funkcji DEC2BIN, jak określić liczbę bitów oraz jak unikać typowych błędów, które mogą pojawić się podczas konwersji. Oprócz tego, omówimy, jak radzić sobie z liczbami ujemnymi oraz jak konwertować liczby binarne z powrotem na dziesiętne za pomocą funkcji BIN2DEC.
Najważniejsze informacje:
- Funkcja DEC2BIN umożliwia konwersję liczb dziesiętnych na binarne w Excelu.
- Można określić liczbę bitów, co wpływa na wynik konwersji.
- Przekroczenie limitów bitów może skutkować błędami.
- Do reprezentacji liczb ujemnych w systemie binarnym używa się zapisu z dopełnieniem do dwóch.
- Funkcja BIN2DEC pozwala na konwersję liczb binarnych z powrotem na dziesiętne.
Jak skutecznie używać funkcji DEC2BIN w Excelu do konwersji
Aby przekształcić liczbę dziesiętną na system binarny w Excelu, kluczową funkcją, którą należy wykorzystać, jest DEC2BIN. Funkcja ta pozwala na łatwe i szybkie konwertowanie wartości dziesiętnych na ich odpowiedniki binarne. Aby użyć tej funkcji, wystarczy wpisać liczbę dziesiętną w jednej komórce, na przykład A1, a następnie w innej komórce wpisać formułę =DEC2BIN(A1). Po naciśnięciu klawisza Enter Excel wyświetli wynik w formacie binarnym.
Na przykład, jeżeli w komórce A1 znajduje się liczba 13, po zastosowaniu formuły =DEC2BIN(A1) otrzymamy wynik 1101. Funkcja DEC2BIN umożliwia również określenie liczby bitów, co jest istotne w przypadku, gdy potrzebujemy, aby wynik był w określonym formacie. Dodatkowo, warto pamiętać, że jeśli liczba binarna wymaga więcej bitów niż określono w drugim argumencie, funkcja zwróci błąd.
Przykład użycia funkcji DEC2BIN dla liczby dziesiętnej
Rozważmy konkretny przykład konwersji liczby dziesiętnej na binarną. Załóżmy, że chcemy przekształcić liczbę 5 na system binarny. W tym celu wprowadzamy liczbę 5 do komórki A1, a następnie w innej komórce wpisujemy formułę =DEC2BIN(A1). Po naciśnięciu Enter, Excel zwróci wynik 101, co jest binarną reprezentacją liczby dziesiętnej 5.Jeśli chcielibyśmy uzyskać wynik jako 8-bitową liczbę binarną, możemy użyć formuły =DEC2BIN(5, 8). Wówczas Excel zwróci wynik 00000101. Dzięki temu możemy dostosować format wyniku do naszych potrzeb, co jest szczególnie przydatne w programowaniu i obliczeniach komputerowych.
Jak określić liczbę bitów w funkcji DEC2BIN
Podczas korzystania z funkcji DEC2BIN w Excelu, określenie liczby bitów jest kluczowe dla uzyskania oczekiwanego wyniku. Możliwość ta pozwala na dostosowanie formatu binarnego, co jest szczególnie ważne w kontekście obliczeń i programowania. Na przykład, jeśli chcemy, aby wynik był 8-bitowy, musimy podać drugi argument w funkcji. W przeciwnym razie Excel zwróci wynik w formacie, który niekoniecznie spełnia nasze wymagania.
Nieprawidłowe określenie liczby bitów może prowadzić do błędów, zwłaszcza gdy liczba binarna wymaga więcej bitów niż określono. Dlatego warto przemyśleć, ile bitów będzie potrzebnych w danym kontekście, aby uniknąć problemów z konwersją. W poniższej tabeli przedstawiono wyniki funkcji DEC2BIN dla różnych liczb dziesiętnych z różnymi specyfikacjami bitów.
| Liczba dziesiętna | DEC2BIN (bez bitów) | DEC2BIN (8 bitów) |
| 5 | 101 | 00000101 |
| 13 | 1101 | 00001101 |
| 255 | 11111111 | 11111111 |
Błędy związane z limitami bitów w funkcji DEC2BIN
Podczas korzystania z funkcji DEC2BIN w Excelu, przekroczenie limitów bitów może prowadzić do poważnych problemów. Jeśli liczba binarna wymaga więcej bitów niż określono w drugim argumencie funkcji, Excel zwróci błąd. Na przykład, jeżeli spróbujemy użyć =DEC2BIN(255, 8), wynik będzie poprawny, ponieważ 255 mieści się w 8 bitach. Jednak gdy spróbujemy użyć =DEC2BIN(256, 8), otrzymamy błąd, ponieważ 256 wymaga 9 bitów do prawidłowej reprezentacji.
Aby zidentyfikować tego typu błędy, warto zwrócić uwagę na zakres liczb, które można przedstawić w danej liczbie bitów. Zrozumienie, ile wartości można zakodować w określonym formacie binarnym, jest kluczowe. W przypadku 8-bitowej reprezentacji możemy zakodować liczby od 0 do 255. Przekroczenie tego zakresu skutkuje błędem, dlatego zawsze należy upewnić się, że liczba, którą chcemy przekonwertować, mieści się w zadanym limicie bitów.
Jak radzić sobie z liczbami ujemnymi w systemie binarnym
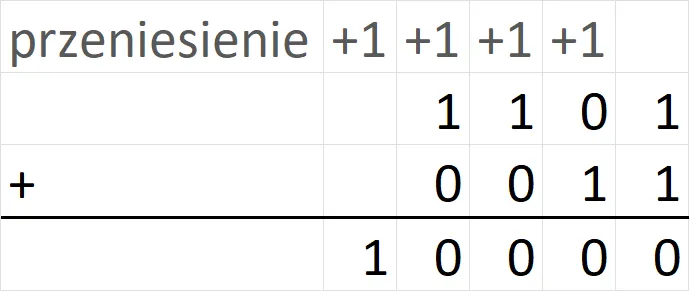
Gdy używamy funkcji DEC2BIN do konwersji liczb ujemnych, musimy zastosować metodę dopełnienia do dwóch. Jest to standardowy sposób reprezentacji liczb ujemnych w systemie binarnym, który pozwala na łatwe wykonywanie operacji arytmetycznych. Na przykład, aby przedstawić liczbę -5 w systemie binarnym jako 8-bitową wartość, najpierw konwertujemy liczbę 5 na binarną, co daje 00000101. Następnie odwracamy wszystkie bity, co daje 11111010, a następnie dodajemy 1, co ostatecznie daje 11111011.
Warto pamiętać, że użycie dopełnienia do dwóch pozwala na reprezentację liczb ujemnych w taki sposób, że zachowujemy spójność w obliczeniach. Dzięki temu, gdy wykonujemy operacje na liczbach binarnych, nie musimy martwić się o dodatkowe zasady dotyczące liczb ujemnych. To podejście jest powszechnie stosowane w programowaniu i obliczeniach komputerowych, co czyni je niezwykle ważnym w kontekście konwersji liczb w Excelu.
Jak konwertować liczby binarne z powrotem na dziesiętne w Excelu
Aby przekształcić liczby binarne z powrotem na dziesiętne w Excelu, należy skorzystać z funkcji BIN2DEC. Funkcja ta przyjmuje jako argument ciąg znaków reprezentujący liczbę binarną i zwraca odpowiadającą jej wartość dziesiętną. Aby użyć tej funkcji, wystarczy wpisać w komórce formułę =BIN2DEC(A1), gdzie A1 to komórka zawierająca liczbę binarną. Po naciśnięciu klawisza Enter, Excel wyświetli wynik w formacie dziesiętnym.
Na przykład, jeśli w komórce A1 znajduje się liczba binarna 1101, użycie formuły =BIN2DEC(A1) zwróci wynik 13, ponieważ 1101 w systemie binarnym odpowiada liczbie 13 w systemie dziesiętnym. To proste narzędzie pozwala na szybkie i efektywne przekształcanie wartości binarnych do formatu, który jest bardziej zrozumiały w codziennych obliczeniach.
Użycie funkcji BIN2DEC do konwersji binarnej na dziesiętną
Funkcja BIN2DEC w Excelu umożliwia łatwe przekształcenie liczby binarnej na jej odpowiednik w systemie dziesiętnym. Na przykład, jeśli mamy liczbę binarną 1101, możemy użyć formuły =BIN2DEC("1101"), aby uzyskać wynik dziesiętny. Po naciśnięciu klawisza Enter Excel zwróci wartość 13, ponieważ 1101 w systemie binarnym odpowiada 13 w systemie dziesiętnym. Jest to bardzo przydatne w obliczeniach, gdy potrzebujemy szybko przekształcić wartości binarne na bardziej zrozumiałe liczby dziesiętne.
Warto również zauważyć, że funkcja BIN2DEC akceptuje liczby binarne zapisane jako ciągi tekstowe, co oznacza, że możemy używać jej do konwersji wartości binarnych wpisanych w komórkach. Poniżej znajduje się lista kilku popularnych liczb binarnych i ich odpowiadających wartości dziesiętnych, co może być pomocne w codziennych obliczeniach.
- 0001 - 1
- 0010 - 2
- 0011 - 3
- 0100 - 4
- 0101 - 5
- 0110 - 6
- 0111 - 7
- 1000 - 8
- 1001 - 9
- 1010 - 10
- 1100 - 12
- 1101 - 13
- 1110 - 14
- 1111 - 15
Czytaj więcej: Co to jest system binarny i dlaczego jest kluczowy w technologii?
Jak wykorzystać konwersję binarną w programowaniu i technologii
Umiejętność konwersji między systemami liczbowymi, takimi jak system binarny i dziesiętny, ma kluczowe znaczenie w programowaniu oraz w różnych dziedzinach technologii. Zrozumienie, jak działają te konwersje, pozwala programistom na efektywniejsze zarządzanie danymi oraz optymalizację algorytmów. Na przykład, w językach programowania, takich jak Python czy C++, konwersje te są często wykorzystywane do manipulacji danymi w formacie binarnym, co jest niezbędne w przypadku pracy z plikami, sieciami czy systemami operacyjnymi.
Dodatkowo, w kontekście rozwoju sztucznej inteligencji i uczenia maszynowego, zrozumienie reprezentacji binarnej danych może znacząco wpłynąć na efektywność modeli. Wiele algorytmów przetwarzania danych opiera się na operacjach binarnych, a optymalizacja tych operacji może prowadzić do znacznych popraw w wydajności. Dlatego warto rozwijać umiejętności związane z konwersją systemów liczbowych, aby lepiej przygotować się na przyszłość w dynamicznie rozwijającym się świecie technologii.

