W kolejnych sekcjach omówimy różnorodne przykłady operacji na bitach, techniki optymalizacji kodu, a także rolę systemu binarnego w przechowywaniu danych. Zrozumienie tych zagadnień jest kluczowe dla każdego, kto pragnie efektywnie pracować z nowoczesnymi technologiami.
Kluczowe wnioski:
- System binarny jest podstawą działania komputerów, reprezentując dane w formie 0 i 1.
- W programowaniu operacje na bitach, takie jak przesunięcia bitowe, są szybsze od tradycyjnych działań arytmetycznych.
- Binary encoding jest kluczowy w kompresji danych, co pozwala na efektywne przechowywanie i przesyłanie informacji.
- Konwersja między systemem dziesiętnym a binarnym jest istotna w wielu zastosowaniach informatycznych.
- W elektronice cyfrowej system binarny wpływa na działanie układów logicznych i urządzeń cyfrowych.
Zastosowanie systemu binarnego w programowaniu i algorytmach
System binarny odgrywa kluczową rolę w programowaniu, umożliwiając wydajne operacje na danych. Wykorzystuje jedynie dwie cyfry – 0 i 1 – co pozwala na reprezentację informacji w sposób zrozumiały dla komputerów. Dzięki tym podstawowym elementom, programiści mogą tworzyć algorytmy, które są zarówno szybkie, jak i efektywne. W szczególności, operacje na bitach są fundamentalne w wielu językach programowania, co czyni je niezbędnymi w codziennej pracy programisty.W praktyce, techniki optymalizacji algorytmów, takie jak przesunięcia bitowe czy operacje logiczne, pozwalają na znaczne przyspieszenie procesów obliczeniowych. Na przykład, w językach takich jak C, C++ czy Python, programiści mogą wykorzystywać operacje bitowe do manipulacji danymi w sposób, który jest bardziej wydajny niż tradycyjne metody. Efektywność tych operacji sprawia, że są one kluczowe w kontekście optymalizacji kodu oraz zwiększania wydajności aplikacji.
Przykłady operacji na bitach w praktycznych zastosowaniach
Operacje na bitach to techniki, które pozwalają na manipulację pojedynczymi bitami w danych. Przykłady takich operacji to AND, OR oraz XOR, które są wykorzystywane do różnych celów, takich jak ustawianie, usuwanie lub sprawdzanie wartości bitów. Dzięki tym operacjom, programiści mogą efektywnie zarządzać danymi i wykonywać obliczenia w sposób, który jest zarówno szybki, jak i oszczędny pod względem zasobów.
W praktyce, operacje te znajdują zastosowanie w wielu językach programowania. Na przykład, w języku C++ można użyć operatora & do wykonania operacji AND, operatora | do operacji OR, a operatora ^ do operacji XOR. Te operacje są nie tylko szybkie, ale również pozwalają na zaawansowane manipulacje danymi, co czyni je niezwykle przydatnymi w codziennej pracy programisty.
| Operacja | Przykład w C++ | Opis |
| AND | result = a & b; | Ustawia bity w wyniku na 1 tylko wtedy, gdy oba bity są 1. |
| OR | result = a | b; | Ustawia bity w wyniku na 1, jeśli przynajmniej jeden z bitów jest 1. |
| XOR | result = a ^ b; | Ustawia bity w wyniku na 1, jeśli bity są różne. |
Jak wykorzystać system binarny w optymalizacji kodu
Optymalizacja kodu przy użyciu systemu binarnego to kluczowa technika, która pozwala programistom na uzyskanie lepszej wydajności aplikacji. Dzięki manipulacji bitami, można znacząco przyspieszyć operacje, które w przeciwnym razie mogłyby być czasochłonne. Wykorzystanie operacji bitowych, takich jak przesunięcia czy operacje logiczne, umożliwia efektywne zarządzanie danymi oraz zmniejsza obciążenie procesora. To sprawia, że system binarny jest nieocenionym narzędziem w arsenale każdego programisty.Jednym z najważniejszych sposobów optymalizacji jest przesunięcie bitowe, które pozwala na szybkie mnożenie lub dzielenie przez potęgę liczby 2. Na przykład, zamiast wykonywać operację mnożenia, można użyć przesunięcia w lewo, co jest znacznie szybsze. Kolejną techniką jest wykorzystanie operacji logicznych, takich jak AND, OR czy XOR, które pozwalają na wydajne porównywanie i modyfikowanie danych. Te metody nie tylko przyspieszają procesy, ale także zmniejszają zużycie pamięci, co jest szczególnie ważne w aplikacjach działających na ograniczonych zasobach.
Warto również zwrócić uwagę na kodowanie uzupełnień do dwóch, które umożliwia reprezentację liczb ujemnych w systemie binarnym. Dzięki tej technice, operacje arytmetyczne, takie jak dodawanie i odejmowanie, mogą być realizowane bez potrzeby dodatkowych instrukcji, co przyspiesza działanie programów. W praktyce, umiejętność stosowania tych technik w codziennym programowaniu może znacząco wpłynąć na efektywność tworzonych aplikacji.System binarny w przechowywaniu i przetwarzaniu danych
System binarny odgrywa kluczową rolę w przechowywaniu i przetwarzaniu danych. Dzięki reprezentacji informacji w postaci 0 i 1, możliwe jest efektywne zarządzanie danymi, co jest niezbędne w nowoczesnych systemach komputerowych. W praktyce, system binarny pozwala na kompresję danych, co znacząco zmniejsza rozmiar plików i przyspiesza ich przesyłanie. Użycie technik kompresji, takich jak kodowanie Huffmana czy LZW, umożliwia ograniczenie ilości miejsca potrzebnego na dysku, co jest szczególnie ważne w dobie rosnących zbiorów danych.
W procesie konwersji danych, system binarny również odgrywa istotną rolę. Konwersja między systemem dziesiętnym a binarnym jest często wykorzystywana w różnych aplikacjach, od programowania po zarządzanie bazami danych. Metody takie jak dzielenie przez 2 czy mnożenie przez potęgi liczby 2 pozwalają na łatwe przekształcanie danych w obie strony. Dzięki tym technikom, użytkownicy mogą efektywnie przetwarzać i analizować dane w różnych formatach.
Rola systemu binarnego w kompresji danych i formatach plików
Kompresja danych to proces, który pozwala na zmniejszenie rozmiaru plików bez utraty jakości informacji. Wykorzystując system binarny, dane są reprezentowane w sposób umożliwiający ich efektywne skompresowanie. Na przykład, formaty plików takie jak JPEG, MP3 czy PNG korzystają z różnych technik kompresji, aby zredukować rozmiar plików, co pozwala na oszczędność miejsca na dysku oraz szybsze przesyłanie danych przez sieć.
Każdy z tych formatów ma swoje unikalne metody kodowania danych. JPEG stosuje stratną kompresję, co oznacza, że część informacji jest tracona w celu zmniejszenia rozmiaru pliku, idealnie nadając się do obrazów. Z kolei MP3 wykorzystuje kompresję stratną dla dźwięku, pozwalając na znaczną redukcję rozmiaru pliku audio. PNG jest formatem bezstratnym, co oznacza, że wszystkie dane są zachowane, ale plik jest większy. Te różnice w kompresji mają kluczowe znaczenie dla użytkowników, którzy muszą wybrać odpowiedni format w zależności od potrzeb.
| Format pliku | Typ kompresji | Średni współczynnik kompresji |
| JPEG | Stratna | 10:1 do 20:1 |
| MP3 | Stratna | 10:1 do 12:1 |
| PNG | Bezstratna | 2:1 do 3:1 |
Konwersja między systemem dziesiętnym a binarnym - techniki i zastosowania
Konwersja między systemem dziesiętnym a binarnym jest kluczowym procesem w informatyce, który umożliwia efektywne przetwarzanie danych. Istnieje kilka technik, które można wykorzystać do tej konwersji, a każda z nich ma swoje praktyczne zastosowania. Najpopularniejszą metodą konwersji z systemu dziesiętnego na binarny jest dzielenie przez 2, które pozwala na uzyskanie reszty i tworzenie reprezentacji binarnej liczby. Z kolei konwersja z systemu binarnego na dziesiętny często polega na mnożeniu przez potęgi liczby 2, co umożliwia obliczenie wartości liczby w systemie dziesiętnym.
W praktyce, konwersja ta ma zastosowanie w wielu dziedzinach, takich jak programowanie, obliczenia matematyczne czy przetwarzanie danych. Zrozumienie metod konwersji jest niezbędne dla osób pracujących z danymi w formacie binarnym, ponieważ wiele systemów komputerowych i aplikacji wymaga tej konwersji do prawidłowego działania. Dodatkowo, znajomość konwersji między tymi systemami jest istotna dla efektywnego zarządzania danymi oraz ich analizowania w różnych kontekstach.
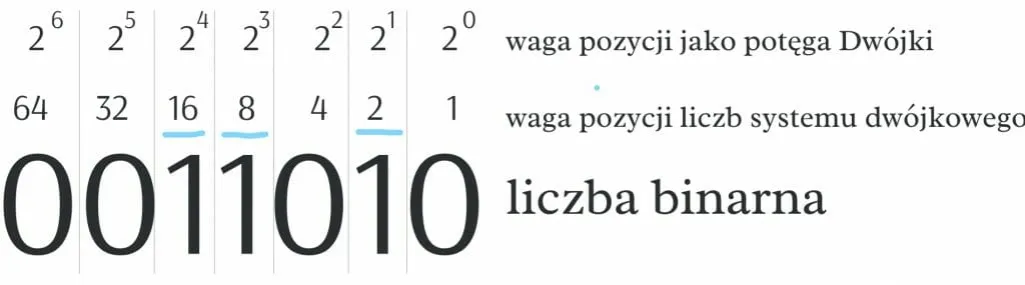
Zastosowanie systemu binarnego w elektronice cyfrowej
System binarny jest fundamentem elektroniki cyfrowej, wpływając na projektowanie i działanie układów logicznych oraz urządzeń. W elektronice, 0 i 1 są używane do reprezentacji stanów w układach logicznych, co umożliwia realizację złożonych operacji obliczeniowych. Dzięki zastosowaniu systemu binarnego, urządzenia elektroniczne mogą wykonywać operacje, takie jak dodawanie, odejmowanie czy porównywanie, w sposób szybki i efektywny. W praktyce, wszystkie nowoczesne urządzenia cyfrowe opierają się na tych zasadach, co czyni system binarny kluczowym elementem ich działania.
Wśród urządzeń, które korzystają z systemu binarnego, można wymienić komputery, smartfony oraz cyfrowe aparaty fotograficzne. Te urządzenia wykorzystują układy logiczne do przetwarzania danych, co pozwala na realizację różnorodnych funkcji, od prostych obliczeń po zaawansowane operacje graficzne. Dzięki systemowi binarnemu, możliwe jest również przechowywanie i przesyłanie informacji w formie cyfrowej, co zrewolucjonizowało sposób, w jaki korzystamy z technologii w codziennym życiu.
Jak system binarny wpływa na działanie układów logicznych
Układy logiczne to podstawowe elementy, które wykorzystują system binarny do realizacji operacji obliczeniowych. Działają na zasadzie przetwarzania sygnałów binarnych, gdzie 0 oznacza stan niski (wyłączony), a 1 stan wysoki (włączony). Dzięki tym sygnałom, układy logiczne mogą podejmować decyzje oraz wykonywać różnorodne operacje, takie jak sumowanie czy porównywanie wartości. Kluczowymi typami układów logicznych są bramki logiczne, które wykonują podstawowe operacje na bitach.
Wśród różnych typów układów logicznych wyróżniamy bramki AND, OR i NOT, które mają swoje specyficzne funkcje. Bramki AND zwracają 1 tylko wtedy, gdy oba wejścia są równe 1. Bramki OR zwracają 1, jeśli przynajmniej jedno z wejść jest równe 1. Natomiast bramki NOT odwracają sygnał, co oznacza, że zwracają 1, gdy wejście wynosi 0, i odwrotnie. Te podstawowe operacje są fundamentem bardziej złożonych układów, które tworzą nowoczesne komputery i inne urządzenia cyfrowe.
| Bramka | Operacja | Wynik (0/1) |
| AND | A i B | 1 tylko, gdy A=1 i B=1 |
| OR | A lub B | 1, gdy A=1 lub B=1 |
| NOT | Nie A | 1, gdy A=0 |
Przykłady zastosowań systemu binarnego w urządzeniach cyfrowych
System binarny znajduje zastosowanie w wielu nowoczesnych urządzeniach cyfrowych, które są nieodłączną częścią naszego życia. Na przykład, komputery wykorzystują system binarny do przetwarzania danych, co pozwala na wykonywanie obliczeń, uruchamianie programów oraz zarządzanie systemami operacyjnymi. Smartfony również opierają swoje działanie na systemie binarnym, umożliwiając komunikację, przetwarzanie multimediów oraz dostęp do Internetu w czasie rzeczywistym.
Innym przykładem są mikrokontrolery, które są używane w różnych urządzeniach, od prostych zabawek po zaawansowane systemy automatyki domowej. Mikrokontrolery przetwarzają dane w formie binarnej, co pozwala na kontrolowanie różnych funkcji, takich jak oświetlenie, temperatura czy bezpieczeństwo. FPGA (Field-Programmable Gate Array) to kolejne urządzenie, które wykorzystuje system binarny do realizacji złożonych funkcji obliczeniowych, co czyni je niezwykle wszechstronnymi w zastosowaniach przemysłowych i badawczych.
- Komputery – przetwarzanie danych i uruchamianie aplikacji.
- Smartfony – komunikacja i dostęp do multimediów.
- Mikrokontrolery – kontrola urządzeń w automatyce domowej.
- FPGA – realizacja złożonych funkcji obliczeniowych w przemyśle.
Przyszłość systemu binarnego w rozwoju technologii kwantowej
W miarę jak technologia kwantowa zyskuje na znaczeniu, system binarny może doświadczyć rewolucji w swoim zastosowaniu. Komputery kwantowe operują na kubitach, które mogą przyjmować wiele stanów jednocześnie dzięki zasadzie superpozycji. To otwiera nowe możliwości w zakresie przetwarzania danych, które mogą być znacznie szybsze i bardziej efektywne niż tradycyjne komputery. W przyszłości, zrozumienie i umiejętność łączenia systemu binarnego z technologią kwantową mogą stać się kluczowymi umiejętnościami dla inżynierów i programistów, którzy będą projektować nowe systemy i aplikacje.
Co więcej, zastosowanie systemu binarnego w kontekście technologii kwantowej może prowadzić do zaawansowanych technik kompresji danych, które wykorzystują złożoność kubitów do efektywnego przechowywania informacji. W miarę jak urządzenia stają się coraz bardziej złożone, umiejętność manipulacji zarówno danymi binarnymi, jak i kwantowymi może stać się niezbędna w tworzeniu innowacyjnych rozwiązań w takich dziedzinach jak sztuczna inteligencja, analiza danych oraz systemy zabezpieczeń. Warto śledzić rozwój tych technologii, aby być na bieżąco z nowymi możliwościami, które mogą wpłynąć na przyszłość elektroniki cyfrowej i przetwarzania danych.

