Kluczowe wnioski:
- System binarny opiera się na dwóch cyfrach: 0 i 1, które są podstawą wszystkich obliczeń komputerowych.
- Każda cyfra w systemie binarnym nazywana jest bitem, a jej wartość jest określana przez pozycję w liczbie.
- Wartości liczb binarnych oblicza się jako sumę potęg liczby 2, co pozwala na efektywne przetwarzanie danych.
- System binarny jest kluczowy w programowaniu, ponieważ wiele języków programowania wykorzystuje go do operacji na danych.
- W cyfrowych układach elektronicznych, 0 i 1 odpowiadają braku i obecności prądu, co umożliwia działanie komputerów.
Jak zbudowany jest system binarny i jego podstawowe zasady
System binarny, znany również jako system dwójkowy, jest najprostszym systemem pozycyjnym, który opiera się na liczbie 2. W tym systemie używamy tylko dwóch cyfr: 0 i 1. Każda cyfra w systemie binarnym nazywana jest bitem, co jest skrótem od terminu binary digit. Wartość liczby w systemie binarnym oblicza się jako sumę potęg liczby 2, odpowiadających pozycjom cyfr, które mają wartość 1. To właśnie dzięki tej prostocie system binarny stał się fundamentem działania komputerów.W systemie binarnym każda kolejna cyfra (licząc od lewej strony) reprezentuje kolejną potęgę liczby 2. Na przykład, liczba binarna 1010 oznacza 1 × 2^3 + 0 × 2^2 + 1 × 2^1 + 0 × 2^0, co daje nam wartość 10 w systemie dziesiętnym. System binarny jest nie tylko prosty, ale również efektywny, ponieważ pozwala na łatwe implementacje w układach cyfrowych, gdzie 0 i 1 odpowiadają braku prądu i jego obecności.
Zrozumienie cyfr binarnych i ich roli w systemie
Cyfry binarne, czyli bity, są podstawowymi jednostkami informacji w systemie binarnym. Każdy bit może przyjmować jedną z dwóch wartości: 0 lub 1. Te dwie wartości są wystarczające do reprezentowania wszelkich danych w komputerze, od tekstu po obrazy. Dzięki zastosowaniu bitów, system binarny umożliwia przechowywanie i przetwarzanie informacji w sposób, który jest zrozumiały dla maszyn.
Jak obliczamy wartości liczb w systemie binarnym
Obliczanie wartości liczb w systemie binarnym polega na przekształceniu binarnej reprezentacji liczby na wartość dziesiętną. W tym celu wykorzystujemy potęgi liczby 2, które odpowiadają pozycjom cyfr w liczbie binarnej. Każda cyfra w liczbie binarnej ma swoją wartość, która jest określona przez to, na jakiej pozycji się znajduje. Na przykład, w liczbie binarnej 1010, pierwsza cyfra od lewej (1) reprezentuje 2^3, druga cyfra (0) to 2^2, trzecia (1) to 2^1, a ostatnia (0) to 2^0.
Aby obliczyć wartość liczby binarnej, sumujemy wartości potęg, które odpowiadają cyfrom równym 1. W przypadku liczby 1010 obliczenia wyglądają następująco: 1 × 2^3 + 0 × 2^2 + 1 × 2^1 + 0 × 2^0 = 8 + 0 + 2 + 0 = 10. Podobnie, możemy obliczyć inne liczby binarne, takie jak 1101 i 1110, które przedstawione w tabeli poniżej pokazują krok po kroku, jak przekształcić je na wartości dziesiętne.
| Liczba binarna | Wartość dziesiętna |
| 1010 | 10 |
| 1101 | 13 |
| 1110 | 14 |
Zastosowanie systemu binarnego w informatyce
System binarny jest kluczowy w informatyce, ponieważ stanowi podstawę dla wszystkich operacji komputerowych. Wykorzystanie systemu binarnego w różnych dziedzinach, takich jak programowanie i projektowanie układów cyfrowych, pozwala na efektywne przetwarzanie danych. Komputery, które operują na danych w formie binarnej, są w stanie wykonywać skomplikowane obliczenia i operacje logiczne w bardzo krótkim czasie. Dzięki temu, system binarny jest fundamentem dla wszystkich nowoczesnych technologii informacyjnych.
W programowaniu, system binarny jest wykorzystywany do reprezentowania danych oraz instrukcji, które komputery rozumieją. Języki programowania, takie jak Python i C++, często operują na wartościach binarnych, co umożliwia programistom tworzenie bardziej wydajnych algorytmów. Na przykład, w Pythonie można używać operatorów bitowych, aby manipulować danymi na poziomie bitów. W C++, programiści mogą korzystać z typów danych binarnych do optymalizacji pamięci i przyspieszenia działania aplikacji.
Rola systemu binarnego w programowaniu i algorytmach
W programowaniu, system binarny odgrywa kluczową rolę w reprezentacji danych oraz w algorytmach. Języki takie jak Python i C++ wykorzystują binarną formę danych do operacji na bitach, co pozwala na tworzenie bardziej efektywnych programów. Na przykład, w Pythonie można łatwo konwertować liczby dziesiętne na binarne za pomocą funkcji bin(), co ułatwia manipulację danymi. Z kolei w C++ operatorzy bitowi, takie jak & (AND), | (OR) i ^ (XOR), pozwalają na wykonywanie operacji logicznych bezpośrednio na poziomie bitów.
Jak system binarny wpływa na działanie układów cyfrowych
System binarny ma kluczowe znaczenie w działaniu układów cyfrowych, ponieważ wszystkie operacje w tych systemach opierają się na dwóch stanach: 0 i 1. Te dwa stany odpowiadają braku i obecności prądu, co pozwala na łatwe przetwarzanie informacji w urządzeniach elektronicznych. W procesorach, które są sercem każdego komputera, instrukcje i dane są reprezentowane w formie binarnej, co umożliwia szybkie wykonywanie obliczeń i operacji logicznych. Pamięci RAM i pamięci stałe również wykorzystują system binarny do przechowywania danych, co zapewnia ich efektywne zarządzanie i dostępność.
W układach cyfrowych, takich jak bramki logiczne, system binarny pozwala na realizację złożonych funkcji logicznych. Na przykład, bramki AND, OR i NOT działają na podstawie wartości binarnych, co umożliwia tworzenie bardziej skomplikowanych układów, takich jak procesory i układy scalone. Dzięki zastosowaniu systemu binarnego, inżynierowie mogą projektować urządzenia, które są zarówno wydajne, jak i niezawodne, co jest kluczowe w dzisiejszym świecie technologii.
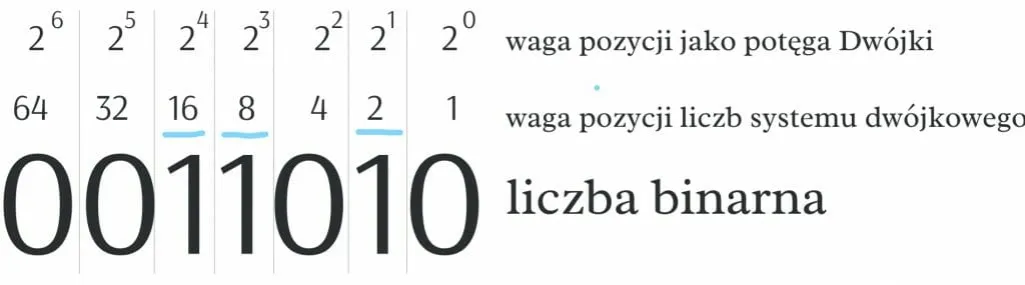
Przykłady konwersji z systemu binarnego na dziesiętny
Konwersja z systemu binarnego na dziesiętny jest procesem, który pozwala na przekształcenie wartości binarnych w bardziej zrozumiałą formę dziesiętną. Istnieje kilka metod, które można wykorzystać do tej konwersji. Najpopularniejszą metodą jest obliczenie wartości każdej cyfry binarnej, mnożąc ją przez odpowiednią potęgę liczby 2. Na przykład, aby przekształcić liczbę binarną 1101 na dziesiętną, wykonujemy obliczenia: 1 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 8 + 4 + 0 + 1 = 13.
Inną metodą konwersji jest użycie tablicy, która przedstawia wartości binarne i ich odpowiedniki dziesiętne. Można również skorzystać z narzędzi online lub funkcji w programach, które automatycznie dokonują takich przekształceń. Na przykład, w Pythonie dostępna jest funkcja int(bina, 2), która konwertuje liczbę binarną na dziesiętną, co znacznie ułatwia proces konwersji dla programistów.
Techniki wizualizacji obliczeń binarnych dla lepszego zrozumienia
Wizualizacja obliczeń binarnych jest kluczowym narzędziem, które pomaga w zrozumieniu, jak działa system binarny. Użycie diagramów, wykresów i tabel może znacząco ułatwić przyswajanie informacji o wartościach binarnych i ich przekształceniu na system dziesiętny. Na przykład, diagramy pokazujące, jak każda cyfra w liczbie binarnej wpływa na jej wartość dziesiętną, mogą pomóc w lepszym zrozumieniu koncepcji potęg liczby 2. Wykresy mogą również ilustrować, jak różne liczby binarne konwertują się na dziesiętne, co może być szczególnie pomocne dla osób uczących się podstaw programowania lub informatyki.
Innym skutecznym narzędziem wizualizacyjnym są interaktywne aplikacje i oprogramowanie, które pozwalają użytkownikom eksperymentować z konwersjami w czasie rzeczywistym. Dzięki nim można szybko zobaczyć efekty zmian w liczbach binarnych i ich odpowiednikach dziesiętnych. Użycie takich narzędzi znacznie przyspiesza proces nauki i sprawia, że obliczenia stają się bardziej przystępne i zrozumiałe.
- Binary Converter - prosta aplikacja online, która szybko przekształca liczby binarne na dziesiętne i odwrotnie.
- Visual Binary - narzędzie do wizualizacji, które pokazuje, jak liczby binarne są reprezentowane w pamięci komputera.
- CalcBin - aplikacja mobilna, która umożliwia użytkownikom ćwiczenie konwersji liczb w różnych systemach liczbowych.
Przyszłość systemu binarnego w technologii i nauce
W miarę jak technologia się rozwija, system binarny staje się coraz bardziej kluczowy w różnych dziedzinach, w tym w sztucznej inteligencji i uczeniu maszynowym. W przyszłości możemy spodziewać się, że algorytmy będą coraz bardziej wykorzystywały binarną reprezentację danych do optymalizacji procesów decyzyjnych. Na przykład, w zastosowaniach związanych z rozpoznawaniem obrazów, systemy binarne mogą być używane do reprezentacji pikseli, co pozwala na szybsze przetwarzanie i analizę danych wizualnych.Dodatkowo, rozwój technologii kwantowych otwiera nowe możliwości dla systemu binarnego. W systemach kwantowych, gdzie informacje są reprezentowane w formie qubitów, które mogą istnieć w wielu stanach jednocześnie, zrozumienie tradycyjnego systemu binarnego staje się kluczowe dla przejścia na bardziej złożone obliczenia. Integracja systemu binarnego z technologią kwantową może prowadzić do znacznych przyspieszeń w obliczeniach, co ma potencjał do rewolucjonizowania wielu branż, od medycyny po inżynierię. Zrozumienie tych trendów może pomóc w przygotowaniu się na przyszłe wyzwania i możliwości w świecie technologii.

