Najważniejsze informacje:
- System binarny opiera się na dwóch cyfrach: 0 i 1, które reprezentują potęgi liczby 2.
- Aby przeliczyć liczbę binarną na dziesiętną, mnożymy każdą cyfrę przez odpowiednią potęgę liczby 2 i sumujemy wyniki.
- Na przykład liczba binarna 101101 przelicza się na 45 w systemie dziesiętnym.
- Można używać narzędzi online, takich jak funkcja BIN2DEC w Excelu, do konwersji między systemami.
- Metoda dzielenia przez 2 jest skutecznym sposobem na konwersję liczb dziesiętnych na binarne.
- System binarny jest kluczowy dla działania komputerów i technologii cyfrowej w codziennym życiu.
Jak odczytać liczby binarne - proste metody dla każdego
Odczytywanie liczb w systemie binarnym jest kluczowe dla zrozumienia, jak działają nowoczesne technologie. System binarny składa się tylko z dwóch cyfr: 0 i 1. Każda cyfra, nazywana bitem, ma swoje miejsce, które odpowiada potędze liczby 2. Zrozumienie tej struktury umożliwia nie tylko odczytywanie danych, ale również ich interpretację w kontekście cyfrowym.
W świecie komputerów, system binarny jest fundamentem, na którym opierają się wszelkie operacje. Każda liczba binarna reprezentuje wartość, która jest sumą potęg liczby 2, w zależności od pozycji cyfr. Dzięki temu, odczytywanie i interpretacja danych stają się znacznie prostsze, co ma ogromne znaczenie w programowaniu oraz w analizie danych.
Zrozumienie podstaw systemu binarnego i jego znaczenie
System binarny ma swoje korzenie w historii matematyki i informatyki. Jego znaczenie wzrosło wraz z rozwojem technologii cyfrowej. Dziś jest powszechnie używany w komputerach, urządzeniach mobilnych i w telekomunikacji. Dzięki zrozumieniu podstaw tego systemu, możemy lepiej pojąć, jak działają urządzenia, z których korzystamy na co dzień.- System binarny jest podstawą wszystkich operacji w komputerach.
- Każda cyfra binarna ma przypisaną wartość odpowiadającą potędze liczby 2.
- Odczytywanie danych w systemie binarnym jest kluczowe dla programowania i analizy danych.
Jak przypisać wartości potęg liczby 2 do cyfr binarnych
Przypisywanie wartości potęg liczby 2 do cyfr binarnych jest kluczowym krokiem w zrozumieniu, jak działa system binarny. Każda cyfra w liczbie binarnej, zwana bitem, ma swoje miejsce, które odpowiada potędze liczby 2. Zaczynamy od skrajnie prawej cyfry, która reprezentuje 2^0, czyli 1. Następnie, idąc w lewo, każda kolejna cyfra zwiększa potęgę o 1, co oznacza, że druga cyfra od prawej to 2^1, trzecia to 2^2, i tak dalej.
Wartości te są używane do obliczenia wartości całkowitej liczby binarnej. Na przykład, w liczbie binarnej 1010, skrajnie prawa cyfra (0) ma wartość 0, a druga cyfra (1) ma wartość 1, co daje 2. W ten sposób możemy zrozumieć, jak każda cyfra przyczynia się do końcowej wartości liczby binarnej, co jest podstawą jej odczytywania i interpretacji.
Konwersja z systemu binarnego na dziesiętny - krok po kroku
Konwersja liczby binarnej na dziesiętną polega na przeliczeniu wartości każdego bitu na odpowiednią potęgę liczby 2. Proces ten zaczynamy od skrajnie prawej cyfry, przypisując jej wartość 2^0. Następnie przechodzimy do kolejnych cyfr, zwiększając potęgę o 1 dla każdej pozycji w lewo. Wartości bitów, które są równe 1, są sumowane, co daje nam wynik w systemie dziesiętnym. Na przykład, dla liczby binarnej 1101, obliczamy: 1×2^3 + 1×2^2 + 0×2^1 + 1×2^0, co daje 8 + 4 + 0 + 1 = 13.
Warto również wspomnieć, że istnieją różne narzędzia i programy, które mogą ułatwić ten proces, takie jak kalkulatory online czy funkcje w arkuszach kalkulacyjnych, które automatycznie przeliczają liczby binarne na dziesiętne. Użycie takich narzędzi może zaoszczędzić czas i zminimalizować ryzyko błędów przy ręcznym obliczaniu. W kolejnych sekcjach omówimy konkretne przykłady konwersji oraz narzędzia, które mogą być użyteczne w tym procesie.
Przykłady konwersji liczby binarnej na dziesiętną
Przykłady konwersji liczb binarnych na dziesiętne mogą pomóc w lepszym zrozumieniu tego procesu. Weźmy na przykład liczbę binarną 1101. Aby przeliczyć ją na system dziesiętny, przypisujemy wartości potęg liczby 2: 1×2^3 + 1×2^2 + 0×2^1 + 1×2^0. To daje nam 8 + 4 + 0 + 1 = 13. Innym przykładem może być liczba binarna 1010, która przelicza się na 2^3 + 0×2^2 + 2^1 + 0×2^0, co daje 8 + 0 + 2 + 0 = 10.
Warto również zwrócić uwagę na liczbę binarną 1110. W tym przypadku obliczenia wyglądają następująco: 1×2^3 + 1×2^2 + 1×2^1 + 0×2^0, co daje 8 + 4 + 2 + 0 = 14. Dzięki tym przykładom można zauważyć, jak każda cyfra w systemie binarnym przyczynia się do wartości końcowej w systemie dziesiętnym, co jest kluczowe w kontekście jak odcyfrowywac system binarny.
Wykorzystanie narzędzi online do konwersji binarnej
W dzisiejszych czasach istnieje wiele narzędzi online, które ułatwiają konwersję liczb binarnych na dziesiętne. Narzędzia te są zazwyczaj proste w obsłudze i pozwalają na szybkie uzyskanie wyników bez potrzeby manualnych obliczeń. Przykłady takich narzędzi to kalkulatory binarno-dziesiętne dostępne na stronach internetowych, które umożliwiają wpisanie liczby binarnej i natychmiastowe uzyskanie jej wartości dziesiętnej. Popularne są również aplikacje mobilne, które oferują podobne funkcje.
Czytaj więcej: Kto wymyślił system binarny? Odkryj jego fascynującą historię
Jak przeliczyć liczby dziesiętne na system binarny - łatwe metody
Przekształcanie liczb dziesiętnych na system binarny jest prostym procesem, który można wykonać na kilka sposobów. Najczęściej stosowaną metodą jest dzielenie przez 2. W tej metodzie dzielimy liczbę dziesiętną przez 2, zapisując resztę z każdego dzielenia. Reszty te, odczytane od dołu do góry, tworzą wynikową liczbę binarną. Na przykład, aby przeliczyć liczbę 13 na system binarny, dzielimy ją przez 2, co daje 6 z resztą 1, następnie 3 z resztą 0, a potem 1 z resztą 1. Ostatecznie, odczytując reszty od dołu do góry, otrzymujemy liczbę binarną 1101.
Kolejną metodą jest wykorzystanie metody potęg liczby 2. W tej metodzie określamy, które potęgi liczby 2 sumują się do danej liczby dziesiętnej. Na przykład, aby przeliczyć 13, zauważamy, że 8 (czyli 2^3) + 4 (czyli 2^2) + 1 (czyli 2^0) daje nam 13. W ten sposób możemy również zapisać liczbę 13 jako 1101 w systemie binarnym. Obie metody są skuteczne i można je stosować w zależności od preferencji użytkownika oraz kontekstu.
Metoda dzielenia przez 2 - krok po kroku
Metoda dzielenia przez 2 to jedna z najprostszych i najczęściej używanych technik konwersji liczb dziesiętnych na binarne. Proces zaczynamy od podzielenia liczby dziesiętnej przez 2. Zapisujemy wynik oraz resztę z dzielenia. Następnie powtarzamy ten krok dla wyniku dzielenia, aż osiągniemy 0. Reszty, które zapisaliśmy, stanowią cyfry binarne, a ich kolejność od ostatniej do pierwszej daje nam ostateczną liczbę binarną. Na przykład, dla liczby 19: dzielimy 19 przez 2, co daje 9 z resztą 1, następnie 9 przez 2 daje 4 z resztą 1, potem 4 przez 2 daje 2 z resztą 0, a 2 przez 2 daje 1 z resztą 0, i na końcu 1 przez 2 daje 0 z resztą 1. Ostatecznie, czytając reszty od dołu do góry, otrzymujemy 10011 jako wynik.
Przykłady konwersji liczby dziesiętnej na binarną
Konwersja liczb dziesiętnych na binarne może być zrozumiana poprzez konkretne przykłady. Rozpocznijmy od liczby 5. Dzieląc ją przez 2, otrzymujemy 2 z resztą 1, następnie 2 dzielimy przez 2, co daje 1 z resztą 0, a na końcu 1 dzielimy przez 2, co daje 0 z resztą 1. Odczytując reszty od dołu do góry, uzyskujemy liczbę binarną 101. Kolejnym przykładem jest liczba 10. Dzielimy ją przez 2, co daje 5 z resztą 0, następnie 5 przez 2 daje 2 z resztą 1, a 2 przez 2 daje 1 z resztą 0, i na końcu 1 przez 2 daje 0 z resztą 1. Ostatecznie, odczytując reszty, otrzymujemy 1010.
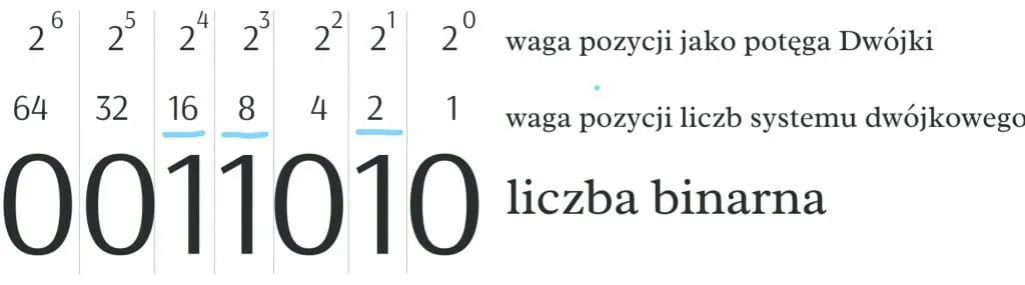
Znaczenie systemu binarnego w technologii i informatyce
System binarny jest fundamentem nowoczesnej technologii i informatyki. W komputerach wszystkie dane, od tekstu po obrazy, są przechowywane i przetwarzane w postaci binarnej. Każdy bit, będący najmniejszą jednostką informacji, może przyjmować wartość 0 lub 1. Dzięki temu komputery mogą wykonywać złożone obliczenia i operacje logiczne, co jest kluczowe dla działania programów i aplikacji, które używamy na co dzień.
W codziennym życiu system binarny ma ogromne znaczenie, zwłaszcza w kontekście komunikacji i przechowywania danych. Na przykład, w sieciach komputerowych informacje przesyłane są w formie sygnałów binarnych, co pozwala na szybkie i efektywne transfery danych. Ponadto, w technologii cyfrowej, takich jak telewizory, smartfony czy urządzenia IoT, system binarny zapewnia podstawę dla działania algorytmów oraz aplikacji, które umożliwiają interakcję z użytkownikami. Dzięki zrozumieniu jak działa system binarny i jego odczyt, możemy lepiej pojąć, jak funkcjonują technologie, które nas otaczają.
Jak wykorzystać system binarny w programowaniu i algorytmach
System binarny ma kluczowe znaczenie nie tylko w podstawowych konwersjach, ale również w programowaniu i tworzeniu zaawansowanych algorytmów. Zrozumienie, jak działa system binarny, umożliwia programistom optymalizację kodu oraz efektywne zarządzanie pamięcią w aplikacjach. Na przykład, w językach programowania, takich jak C czy Python, manipulowanie danymi binarnymi pozwala na szybsze wykonywanie operacji, co jest szczególnie istotne w aplikacjach wymagających dużej wydajności, takich jak gry komputerowe czy systemy czasu rzeczywistego.
Dodatkowo, w kontekście uczenia maszynowego i sztucznej inteligencji, zrozumienie reprezentacji binarnej danych jest kluczowe dla efektywnego przetwarzania informacji. Algorytmy uczenia maszynowego często operują na dużych zbiorach danych, a ich efektywność można zwiększyć poprzez optymalizację reprezentacji binarnej. Na przykład, techniki takie jak kompresja danych lub kodowanie binarne mogą znacznie przyspieszyć procesy uczenia i predykcji. W przyszłości, rozwój technologii kwantowych może jeszcze bardziej zrewolucjonizować sposób, w jaki wykorzystujemy system binarny, otwierając nowe możliwości w obliczeniach i analizie danych.

